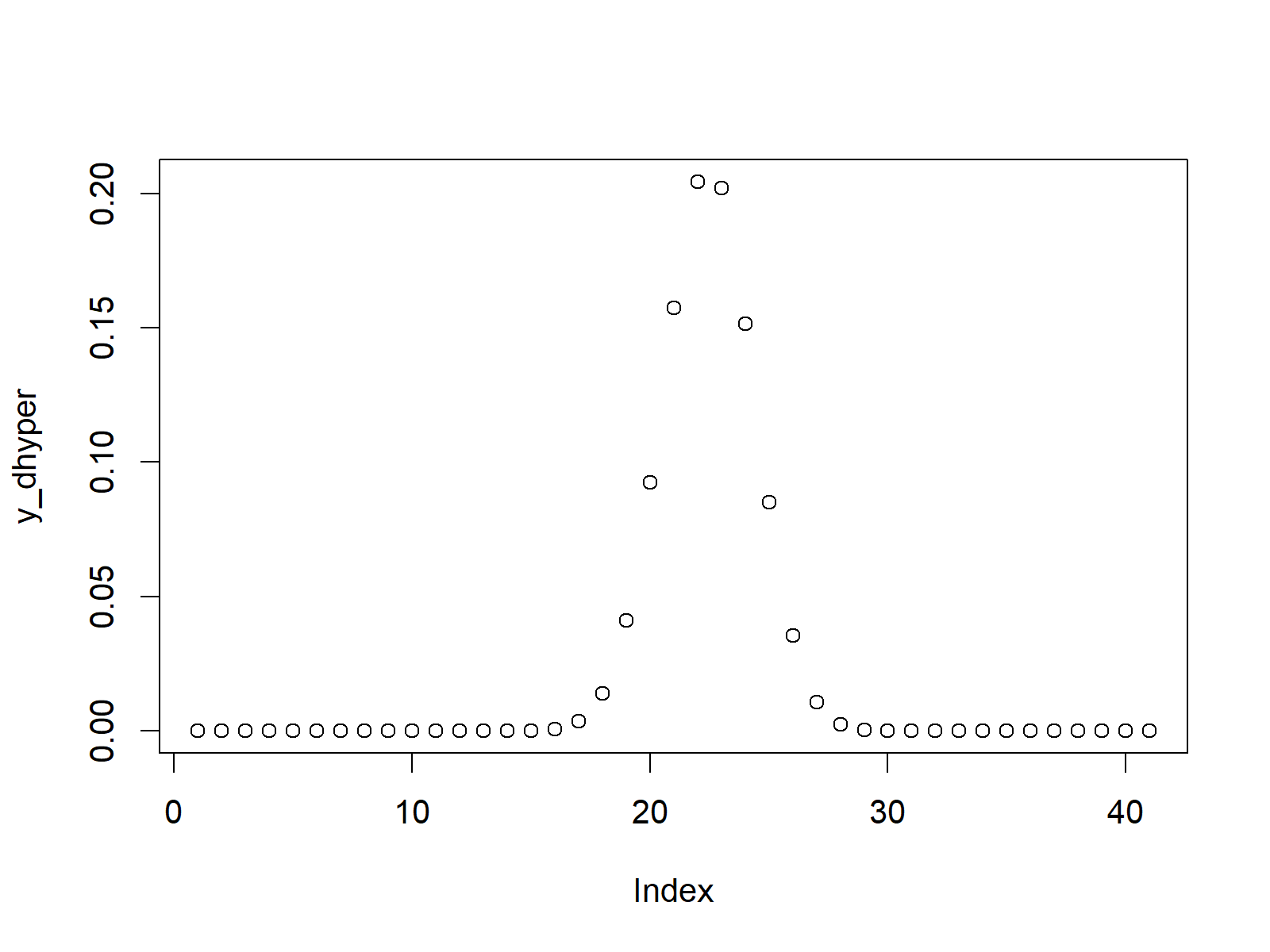
La distribución hipergeométrica se usa para modelar el número de éxitos en una muestra de tamaño n de una población de tamaño N en la que se sabe que hay K éxitos.
La Distribución Hipergeométrica se usa cuando se seleccionan muestras aleatorias sin reemplazo de una población finita y se está interesado en la proporción de una característica particular de la muestra.
La función dhyper() en R se usa para calcular la densidad de probabilidad de la Distribución Hipergeométrica, la función phyper() se usa para calcular la función de distribución acumulada de la Distribución Hipergeométrica, la función qhyper() se usa para calcular el valor cuantil de la Distribución Hipergeométrica y la función rhyper() se usa para generar números aleatorios de la Distribución Hipergeométrica.
Ejemplo 1:
Supongamos que tenemos una población de 10 elementos, de los cuales 4 son rojos y 6 son negros. Si seleccionamos una muestra aleatoria de 3 elementos, ¿cuál es la probabilidad de que la muestra contenga 2 elementos rojos y 1 elemento negro?
Podemos calcularlo usando la función dhyper():
dhyper(2,4,6,3)
Ejemplo 2:
Supongamos que tenemos una población de 10 elementos, de los cuales 4 son rojos y 6 son negros. Si seleccionamos una muestra aleatoria de 3 elementos, ¿cuál es la probabilidad de que la muestra contenga 1 elemento rojo y 2 elementos negros?
Podemos calcularlo usando la función dhyper():
dhyper(1,4,6,3)
Ejemplo 3:
Supongamos que tenemos una población de 10 elementos, de los cuales 4 son rojos y 6 son negros. Si seleccionamos una muestra aleatoria de 3 elementos, ¿cuál es la probabilidad de que la muestra contenga 3 elementos negros?
Podemos calcularlo usando la función dhyper():
dhyper(0,4,6,3)
Ejemplo 4:
Supongamos que tenemos una población de 10 elementos, de los cuales 4 son rojos y 6 son negros. Si seleccionamos una muestra aleatoria de 3 elementos, ¿cuál es la probabilidad de que la muestra contenga al menos 2 elementos rojos?
Podemos calcularlo usando la función phyper():
phyper(1,4,6,3)
Principales diferencias entre las funciones dhyper, phyper, qhyper y rhyper
En estadística, las funciones hipergeométricas se utilizan para calcular la probabilidad de que un determinado número de éxitos ocurra en una muestra de tamaño fijo, cuando se selecciona al azar de una población de tamaño fijo. Estas funciones se llaman funciones hipergeométricas debido a que la distribución hipergeométrica es la distribución de probabilidad de una variable aleatoria que describe el número de éxitos en una muestra de tamaño fijo, seleccionada al azar de una población de tamaño fijo.
Hay cuatro funciones hipergeométricas principales:
-dhyper: calcula la probabilidad de que un determinado número de éxitos ocurra en una muestra.
-phyper: calcula la probabilidad de que un número igual o menor de éxitos ocurra en una muestra.
-qhyper: calcula la probabilidad de que un número igual o mayor de éxitos ocurra en una muestra.
-rhyper: genera un número aleatorio que sigue una distribución hipergeométrica.
La función dhyper se utiliza para calcular la probabilidad de que un determinado número de éxitos ocurra en una muestra. La función phyper se utiliza para calcular la probabilidad de que un número igual o menor de éxitos ocurra en una muestra. La función qhyper se utiliza para calcular la probabilidad de que un número igual o mayor de éxitos ocurra en una muestra. La función rhyper se utiliza para generar un número aleatorio que sigue una distribución hipergeométrica.
¿Cómo se aplica la distribución hipergeométrica en R para resolver problemas reales?
La distribución hipergeométrica se utiliza en R para resolver problemas reales de dos maneras principales. En primer lugar, se puede utilizar para determinar si un cierto número de objetos en una muestra seleccionada al azar se originan de un grupo particular de objetos. En segundo lugar, se puede utilizar para estimar la probabilidad de que un determinado número de objetos en una muestra seleccionada al azar se originen de un grupo particular de objetos.
¿Cómo calcular la probabilidad de éxito de una muestra de tamaño determinado con la distribución hipergeométrica en R?
La distribución hipergeométrica es una distribución de probabilidad discreta que se usa para modelar el número de «éxitos» en una muestra de tamaño determinado, tomada de una población de tamaño finito en la que se sabe la proporción de «éxitos».
La función hipergeométrica en R se puede calcular utilizando la función «dhyper» del paquete «stats». La sintaxis de la función es la siguiente:
dhyper(x, m, n, k)
donde:
x = el número de «éxitos» en la muestra
m = el número de «éxitos» en la población
n = el tamaño de la muestra
k = el tamaño de la población
Por ejemplo, supongamos que tenemos una población de 10.000 personas, de las cuales 1.000 son mujeres. Si tomamos una muestra aleatoria de 100 personas, ¿cuál es la probabilidad de que la muestra contenga exactamente 50 mujeres?
Para calcular esto, necesitamos los valores de x, m, n, k:
x = 50 (porque queremos encontrar la probabilidad de exactamente 50 mujeres en la muestra)
m = 1.000 (porque hay 1.000 mujeres en la población)
n = 100 (porque la muestra es de tamaño 100)
k = 10.000 (porque la población es de tamaño 10.000)
Así que la sintaxis de la función sería:
dhyper(50, 1000, 100, 10000)
y el resultado sería:
0.07142857
La Distribución hipergeométrica se utiliza en estadística para modelar el número de «éxitos» en una muestra de tamaño «n», donde se conoce el número total de «éxitos» y el tamaño total de la población. En R, la función «dhyper» calcula la función de densidad de probabilidad de la distribución hipergeométrica, «phyper» calcula la función de distribución de probabilidad, «qhyper» calcula la función inversa de la función de distribución de probabilidad y «rhyper» genera números aleatorios que siguen una distribución hipergeométrica.
La distribución hipergeométrica se puede utilizar para describir el número de objetos de una cierta clase que se obtiene al seleccionar aleatoriamente una muestra de objetos de una población.
En la teoría de la probabilidad y la estadística, la distribución hipergeométrica es una distribución de probabilidad discreta que describe el número de éxitos en una muestra aleatoria sin reemplazo de tamaño n de una población de tamaño N con un número fijo de éxitos.
La función dhyper calcula la densidad de probabilidad, la función phyper calcula la función de distribución acumulada, la función qhyper calcula el cuantil y la función rhyper genera muestras aleatorias.
Alejandro Lugón es un economista y escritor especializado en Python y R, conocido por ser el creador del blog Estadisticool. Nacido en México, Lugón se graduó de la Universidad Autónoma de México con una Licenciatura en Economía. Desde entonces ha trabajado como economista en varias empresas. Lugón también ha escrito varios libros sobre temas relacionados con la economía, el análisis de datos y la programación. Su blog Estadisticool se ha convertido en un lugar de referencia para los programadores de Python y R. Alejandro Lugón es una inspiración para aquellos que buscan aprender programación y análisis de datos. Su trabajo ha ayudado a muchas personas a entender mejor el uso de la tecnología para hacer sus trabajos.